- 今回の問題
- 解説
- コンプトン散乱における基本公式
- 問題文の理解
- 解法
- 問題文より、散乱光子 hν’ =反跳電子 K を条件に基本公式⑴式を変形する
- 得られた関係式を基本公式⑵式に代入して散乱角θを求める
- 解説
今回の問題
今回は令和3年度第1種放射線取扱主任者試験「物理学」よりコンプトン散乱の散乱角についての問題を解説していきます。
なお、問題文は原子力安全技術センターHPより引用しております。
問21
1.02MeVのγ線が物質でコンプトン散乱を起こした場合、散乱光子と反跳電子のエネルギーが同じであった。この場合、散乱角として最も近い値はどれか。
1. 30°
2. 45°
3. 60°
4. 75°
5. 90°
解説
コンプトン散乱における基本公式
下図のようなコンプトン散乱を想定した場合以下の式が成り立つ
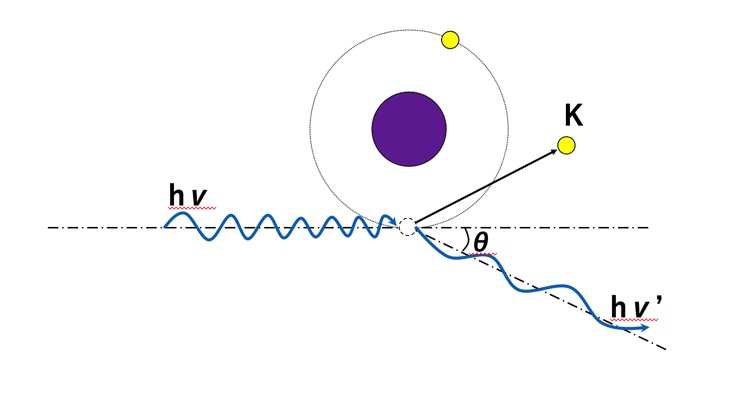
- $$ hν = hν’ + K $$
- $$hν’=\frac{hν}{1+\frac{hν}{m_{o}c^2}(1-cosθ)}$$
hν:入射光子
hν’:散乱光子
K:反跳電子
θ:散乱角
問題文の理解
この問題はコンプトン散乱においての散乱角についての問題です。
- 問題文より、散乱光子 hν’ =反跳電子 K を条件に基本公式⑴式を変形する
- 得られた関係式を基本公式⑵式に代入して散乱角θを求める
解法
問題文より、散乱光子 hν’ =反跳電子 K を条件に基本公式⑴式を変形する
反跳電子と散乱光子のエネルギーが等しい為 K = hν’ として基本公式⑴式に代入する
$$hν = 2hν’ $$
ここで計算しやすいように\(hν’ = \frac{1}{2}hν \)とする・・・(a)
得られた関係式を基本公式⑵式に代入して散乱角θを求める
(a)を⑵式へ代入して整理すると
$$hν’=\frac{1}{2}hν=\frac{hν}{1+\frac{hν}{m_{o}c^2}(1-cosθ)}$$
$$\frac{1}{2}=\frac{1}{1+\frac{hν}{m_{o}c^2}(1-cosθ)}$$
ここで両辺の分母に注目すると
$$2=1+\frac{hν}{m_{o}c^2}(1-cosθ)$$
これを計算すれば良い。
$$1=\frac{hν}{m_{o}c^2}(1-cosθ)$$
$$\frac{m_{o}c^2}{hν}=1-cosθ$$
$$cosθ=1-\frac{m_{o}c^2}{hν}$$
問題文よりhν=1.02MeV、\(m_{o}c^2\)は0.511MeVより
$$cosθ=\frac{1}{2}$$
よってθ=60°となり、選択肢は【3】になります
お疲れさまでした。


コメント