我们在弹琴、唱歌、作曲、编曲时都会与Do Re Mi Fa So La Xi接触，甚至于现实生活中任何有音高的声音都可以用它们表达出来。那它们究竟是怎么来的呢？

其实，七个音是由调律法所产生的，现代所用比较广泛的调律法有五度相生律、纯律、十二平均律。本文重点介绍五度相生律和十二平均律。        

五度相生律，是由毕达哥拉斯计算并整理得出的，故又称为毕达哥拉斯律（其实我们中国的老祖宗管仲比他还早就提出了这个概念以及算法，只不过我们称之为“三分损益法”）。顾名思义，五度相生律即以五度的关系相互衍生，再做适当移动，最后得出一个八度以内的七个音。毕达哥拉斯是古希腊数学家，所以他就发挥了学科优势，依靠比例算出了七个音。       

毕达哥拉斯靠1:2的比例发现了八度这一重要概念。具体步骤如下，我们假定有一根可以发出400Hz的琴弦（以整数400Hz为例，方便后面计算），拨动该弦发出第一个声音，记为X；再将弦对折，然后拨动发出另一个声音，记为2X；重复上述操作可得出4X，8X，16X的音，即400Hz、800Hz、1600Hz、3200Hz、6400Hz的音，他们听起来会是这个样子：（为了阻止泛音的影响，我们的音频示例均采用正弦波）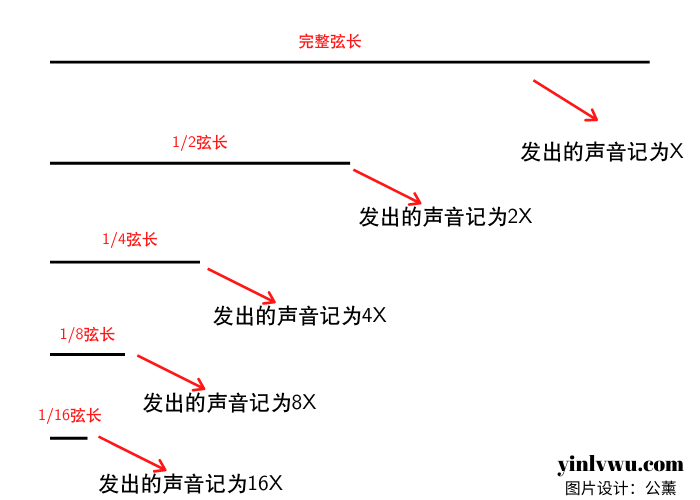

通过音频我们可以听出这些音都是同一个音，只是他们的音高不同。例如红色可以分为粉红、大红、紫红、深红，一样的道理，他们都是同一样东西的不同版本。

现在我们有了八度的概念，就可以将研究范围缩小到一个八度之内，如X~2X之间。通过1:2我们确定了八度，那么通过其他比例可不可以得到其他音呢？答案是可以的，毕达哥拉斯崇尚数学的简洁美，于是下一个比例用了2:3，这会发生什么神奇的事呢？

实际上，这个音就是So，只是在毕达哥拉斯那个时代他并不知道这个音是So（七个音的命名是后来由一名意大利人和一名比利时人发明并补充完成的，那是另外一个故事了，在此不多赘述），他只知道通过2:3产生了一个新的音。        

依据五度相生律，我们得出了第一个五度音So，继续在3X/2的基础上按照2:3的比例可得出第二个五度音Re。在此过程中要遵循一个计算原则：当所得频率超过2X时，要除以2将其移回一个八度内。如下：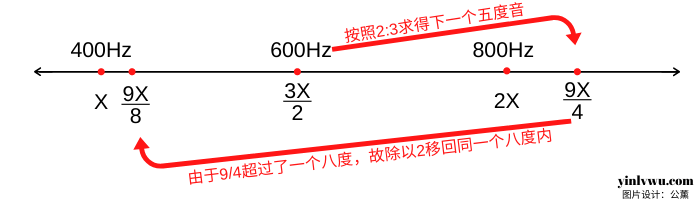

懂了以上原理之后就可以继续按照2:3的比例算出所有七个音（如果看不懂的同学，建议亲自动手算呢）。笔者的计算结果如下：

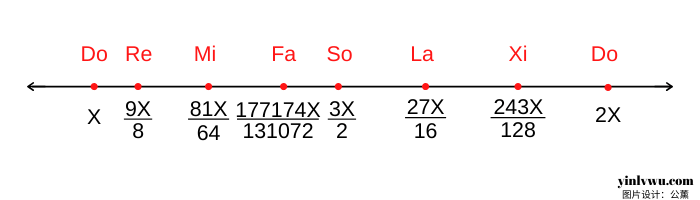
转换为表格如下图：

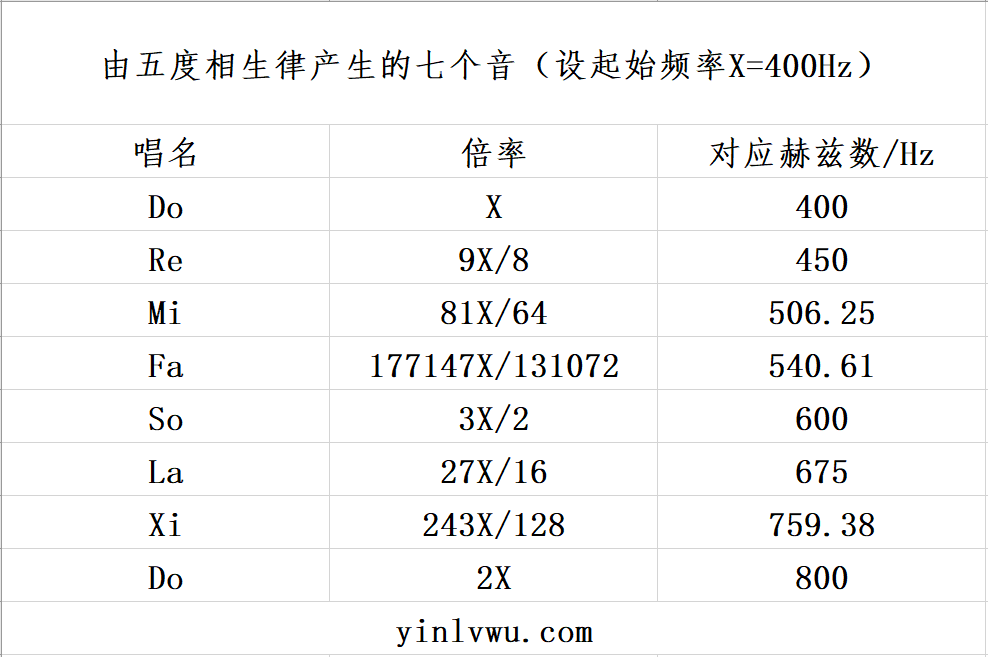
听起来已经非常接近现代的自然大调了，然而随着历史的发展，到了巴赫时期，作曲家们需要大量的使用转调，而五度相生律所产生的七个音地位不平等，并且还存在“狼五度——Wolf Fifth”这么一个十分不协和的音程（篇幅有限，同学们可自行了解“狼五度”），因此五度相生律只适合旋律式写作。为了适应转调，于是就诞生了十二平均律！        

十二平均律，顾名思义，就是将一个八度均分为12份，每一份即一个半音。由于是均分的，每一个音具有同等地位，故适用于转调歌曲。理论很完美，但是由于当时的科学计算能力不足，人们找不到这么一个频率比例可以将一个八度均分为12份。如今，我们能够轻松地依靠手机计算器找到这个数即：2的12次方根。到这里需要一点数学理解能力，均分为12份即X连乘12次2的12次方根之后要等于2X。（咨询了数学系的同学，这里的均分并不是数学意义上的均分，大可不必太钻牛角尖。）
省略#记号的变化音，我们只讨论单纯的七个音，转换为表格如下图：

其实十二平均律最早是由我国明代大音乐家朱载堉发明的，这一发明早于西方500多年，并且最令人佩服的是，他还利用算盘算出了2的12次方根，由此，将这一发明留在了中国，可见先人的智慧着实令人佩服！如今，十二平均律应用广泛，钢琴调律就是以十二平均律为基准的。        

最后，我们比较一下，由五度相生律和十二平均律所产生的七个音之间的误差。

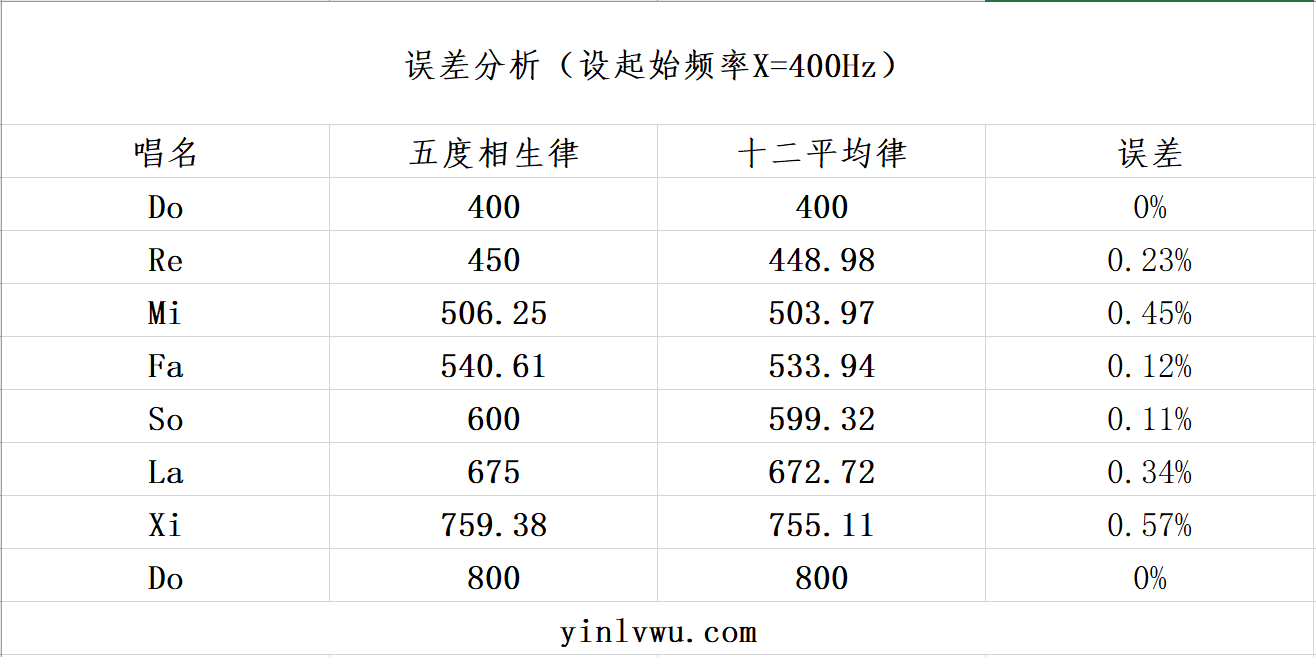
由此可见，两者相差其实不大，一般人较难听出两者的区别，但是音乐是客观的，这点细微的差别也可能导致歌曲的色彩不同。

尾记：调律法是一个很大的课题，本文只介绍了两种常见的，还有许多有趣的律法，感兴趣的同学可以继续去了解。